Matemática Financeira (com regra de 3)

infinito dividido por infinito - Para dar sorte

1. A tabela a seguir apresenta alguns resultados aproximados para 1,07n em função de n.

Ainda que as potências não aumentem de forma linear, é possível obter uma boa aproximação para 1,076,2 por meio de regra de três aplicada sobre os intervalos entre os valores apresentados.
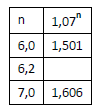
Aplicando-se essa técnica, a aproximação obtida é:

A) 1,508;

B) 1,510;

C) 1,522;

D) 1,530;

E) 1,535.

Podemos fazer dessa forma, o valor de (1,07^6,2), sendo o ^ elevado, teremos o valor de 'x'.

Se pegarmos o 6,2 e diminuir 6,0, linearmente seria o mesmo que diminuir x e 1,501.

Se pegarmos o 7,0 e diminuir 6,2, linearmente seria o mesmo que diminuir 1,606 e x. 

Pelos valores serem lineares entre si, podemos colocar essas expressões em igualdade:

Multiplicando em formato de x:

0,2 . (1,606 – x) = 0,8 . (x – 1,501)

0,3212 – 0,2x = 0,8x – 1,2008

0,8x + 0,2x = 0,3212 + 1,2008

1x = 1,522

x = 1,522

Como x é o valor de 1,07 elevado a 6,2, como fizemos desde o início, essa é a resposta: x = 1,522:

Letra C).